Pfthb

Die Zirkulation ist das Umlaufintegral eines Vektorfeldes über einen geschlossenen Weg. Bei Strömungen ist sie ein Maß für die Wirbelstärke in dem vom Weg umschlossenen Gebiet.

Der Begriff wird in der Vektoranalysis, in der Strömungslehre und in der Elektrodynamik benutzt. Die Zirkulation kommt insbesondere im Satz von Stokes vor, der eine zentrale Rolle in der Elektrodynamik spielt.

Mathematische Formulierung |

Ist Wdisplaystyle W ein stückweise glatter, geschlossener und orientierter Weg im Rndisplaystyle mathbb R ^n (von besonderer Bedeutung ist hier der R3displaystyle mathbb R ^3) und v→displaystyle vec v ein längs dieses Weges integrierbares Vektorfeld, so heißt

∮W⁡v→(r→)⋅dr→displaystyle oint _Wvec v(vec r)cdot mathrm d vec r

Zirkulation von v→displaystyle vec v längs Wdisplaystyle W.

Ist ein Vektorfeld v→displaystyle vec v auf einer orientierten und stückweise glatt berandeten Fläche Adisplaystyle A differenzierbar, so ist nach dem Satz von Stokes die Zirkulation von v→displaystyle vec v längs des zu Adisplaystyle A gehörigen orientierten Randes ∂Adisplaystyle partial A gleich dem Flächenintegral der Rotation von v→displaystyle vec v über Adisplaystyle A:

∮∂A⁡v→⋅dr→=∫Arotv→⋅dA→.displaystyle oint _partial Avec vcdot mathrm d vec r=int _A;operatorname rot ;vec vcdot mathrm d vec A.

Die komplexe Zirkulation |

Wenn das Vektorfeld in einer Ebene liegt, dann können die Eigenschaften komplexer Funktionen ausgenutzt werden. Dazu wird das Vektorfeld als komplexe Funktion w(z)displaystyle w(z) aufgefasst, deren Real- und Imaginärteile die Komponenten des Vektorfeldes sind, dessen Ebene als Gauß’sche Zahlenebene modelliert wird, in der die komplexe Zahl zdisplaystyle z einen Punkt markiert. Die komplexe Zirkulation ist dann das komplexe Kurvenintegral der komplexen Funktion w(z)displaystyle w(z) längs einer Kurve Wdisplaystyle W in der Ebene. Der Realteil der komplexen Zirkulation ist die oben eingeführte reelle Zirkulation längs des Weges Wdisplaystyle W, also das Integral über die Komponente des Vektorfeldes, die tangential zur Kurve ist. Der Imaginärteil ist hingegen das Integral über die Komponente des Vektorfeldes, die senkrecht zur Kurve ist.

Besondere Regeln gelten, wenn die komplexe Funktion w(z)displaystyle w(z) eine holomorphe Funktion ist. Wenn der Weg Wdisplaystyle W ein Gebiet umfasst, in dem die Funktion w(z)displaystyle w(z) überall holomorph ist, dann verschwindet die komplexe Zirkulation längs des Weges Wdisplaystyle W identisch. Wenn Kdisplaystyle K eine weitere Kurve ist, die den Weg Wdisplaystyle W einschließt, und die Funktion w(z)displaystyle w(z) im Gebiet zwischen den Kurven Kdisplaystyle K und Wdisplaystyle W holomorph ist, dann ist die Zirkulation der Funktion w(z)displaystyle w(z) längs der Kurve Kdisplaystyle K gleich ihrer Zirkulation längs der Kurve Wdisplaystyle W.

Diese Aussagen werden im Folgenden begründet.

Definition |

Sei

w(z):=vx(x,y)−ivy(x,y)mitz=x+iydisplaystyle w(z):=v_x(x,y)-mathrm i ,v_y(x,y)quad textmitquad z=x+mathrm i ,y

die komplexe Funktion mit Komponenten vx,ydisplaystyle v_x,y des Vektorfeldes bezüglich eines kartesischen x-y-Koordinatensystems in der Gauß’schen Zahlenebene mit idisplaystyle mathrm i als imaginärer Einheit.

Die komplexe Zirkulation der Funktion wdisplaystyle w längs des Weges Wdisplaystyle W ist dann das komplexe Wegintegral

ΓC:=∮W⁡w(z)dz.displaystyle Gamma _C:=oint _Ww(z),mathrm d z,.

Real- und Imaginärteil der komplexen Zirkulation |

Bogenlängendarstellung der Kurve W mit Tangenten- und Normalenvektor

Einsetzen der komplexen Funktion ergibt den Real- und den Imaginärteil:

ΓC=∮W⁡w(z)dz=∮W⁡(vx−ivy)(dx+idy)=∮W⁡(vxdx+vydy)+i∮W⁡(vxdy−vydx)=:Γ+iQ.displaystyle beginalignedGamma _C&=oint _Ww(z),mathrm d z=oint _W(v_x-mathrm i ,v_y)(mathrm d x+mathrm i ,mathrm d y)\&=oint _W(v_x,mathrm d x+v_y,mathrm d y)+mathrm i oint _W(v_x,mathrm d y-v_y,mathrm d x)=:Gamma +mathrm i ,Q,.endalignedGamma_C
&="oint_W w(z),mathrmdz"
="oint_W (v_x-mathrmi,v_y)(mathrmdx+mathrmi,mathrmdy)"
\&="oint_W (v_x,mathrmdx+v_y,mathrmdy)+mathrmioint_W(v_x,mathrmdy-v_y,mathrmdx)"
=":Gamma + mathrmi,Q,."
endalign"/>

Der Realteil

Γ=∮W⁡(vxdx+vydy)=∮W⁡v→⋅dx→⏟=x→′ds=∫0lv→⋅x→′dsdisplaystyle Gamma =oint _W(v_x,mathrm d x+v_y,mathrm d y)=oint _Wvec vcdot underbrace mathrm d vec x _=vec x',mathrm d s=int _0^lvec vcdot vec x',mathrm d s="oint_W (v_x,mathrmdx+v_y,mathrmdy)"
="oint_W vecvcdotunderbracemathrmdvecx_=vecx',mathrmds"
="int_0^l vecvcdotvecx',mathrmds"
"/>

ist die oben eingeführte reelle Zirkulation längs des Weges Wdisplaystyle W in der Ebene. Die senkrecht zur Ebene zählenden Komponenten der hier vorkommenden Vektoren verschwinden nach Voraussetzung: v→=(vx,vy,0),dx→=(dx,dy,0),…displaystyle vec v=(v_x,v_y,0),,;mathrm d vec x=(mathrm d x,mathrm d y,0),ldots Die Kurve Wdisplaystyle W wurde oben gemäß W:s∈[0,l)↦x→(s)displaystyle Wcolon sin [0,l)mapsto vec x(s) mit der Bogenlänge sdisplaystyle s parametrisiert, so dass ldisplaystyle l die Länge der Kurve ist und der Betrag des Tangentenvektors x→′displaystyle vec x' gleich eins ist, worin der Strich für die Ableitung nach der Bogenlänge steht.

Der Imaginärteil der komplexen Zirkulation ist gemäß

Q:=∮W⁡(vxdy−vydx)=−∮W⁡v→⋅(e^×dx→)=∫0lv→⋅(x→′×e^)ds=∫0lv→⋅n^dsdisplaystyle Q:=oint _W(v_x,mathrm d y-v_y,mathrm d x)=-oint _Wvec vcdot (hat etimes mathrm d vec x)=int _0^lvec vcdot (vec x'times hat e),mathrm d s=int _0^lvec vcdot hat n,mathrm d s="-oint_W vecvcdot(hatetimesmathrmdvecx)"
="int_0^l vecvcdot(vecx'timeshate),mathrmds"
="int_0^l vecvcdothatn,mathrmds"
"/>

das Integral über die Komponenten des Vektorfeldes normal zur Kurve. Der Vektor e^:=(0,0,1)displaystyle hat e:=(0,0,1) hat den Betrag eins und steht senkrecht auf der Ebene, so dass x→′×e^=n^displaystyle vec x'times hat e=hat n die Normale an der Kurve ist, siehe Bild. Das Rechenzeichen ×displaystyle times bildet das Kreuzprodukt.

Wenn die Funktion w(z)displaystyle w(z) eine komplexe Strömungsgeschwindigkeit ist und der Weg Wdisplaystyle W eine umströmte Wand darstellt, dann wird sie nicht durchflossen und die komplexe Zirkulation der komplexen Geschwindigkeit w(z)displaystyle w(z) längs der Kontur Wdisplaystyle W ist reell.

Zirkulation holomorpher Funktionen |

Der Integralsatz von Cauchy besagt, dass das Kurvenintegral einer komplexen Funktion zwischen zwei Punkten wegunabhängig ist, wenn die Funktion holomorph also komplex differenzierbar ist. Das Kurvenintegral verschwindet demnach entlang einer geschlossenen Linie immer, wenn die Funktion in dem von der Linie umschlossenen Gebiet holomorph ist. Die Zirkulation einer Funktion entlang einer Linie kann also nur dann von null verschieden sein, wenn die Funktion irgendwo innerhalb der Linie nicht komplex differenzierbar ist.

Integrationsweg, der die Kurven W und K einschließt

Für die Berechnung der Zirkulation macht es keinen Unterschied, ob sie entlang eines Weges Wdisplaystyle W oder entlang eines anderen Weges Kdisplaystyle K, der den Weg Wdisplaystyle W umschließt, berechnet wird, sofern die Funktion im Gebiet zwischen den Wegen Kdisplaystyle K und Wdisplaystyle W holomorph ist, siehe Bild. Wenn die Funktion w(z)displaystyle w(z) im gelb gezeichneten Gebiet holomorph ist, dann gilt nach dem Integralsatz von Cauchy:

∫Ww(z)dz+∫Aw(z)dz−∫Kw(z)dz−∫Bw(z)dz=0.displaystyle int _Ww(z),mathrm d z+int _Aw(z),mathrm d z-int _Kw(z),mathrm d z-int _Bw(z),mathrm d z=0,.

Die Beiträge der Wege Kdisplaystyle K und Bdisplaystyle B gehen mit umgekehrtem Vorzeichen ein, weil bei ihnen der Integrationsweg gegenüber den Wegen Wdisplaystyle W und Adisplaystyle A – wie im Bild angedeutet – gegensinnig durchlaufen wird. Geht die Linie Adisplaystyle A in Bdisplaystyle B über, dann heben sich ihre beiden Beiträge auf, die Wege Wdisplaystyle W und Kdisplaystyle K werden geschlossen und es ergibt sich, dass die Zirkulation der Funktion w(z)displaystyle w(z) längs des Weges Wdisplaystyle W gleich der längs des Weges Kdisplaystyle K ist:

∫Ww(z)dz=∫Kw(z)dz.displaystyle int _Ww(z),mathrm d z=int _Kw(z),mathrm d z,.

Für den Weg Kdisplaystyle K kann beispielsweise – wie im Bild – ein Kreis genommen werden, wenn dieser für die Berechnung geeigneter ist.

Beispiel |

Zirkulation des Magnetfeldes eines Stromfadens |

Ein auf der zdisplaystyle z-Achse liegender Stromfaden, der in positiver zdisplaystyle z-Richtung mit dem Strom Idisplaystyle I durchflossen ist, wird von dem Magnetfeld

H→(r,φ,z)=e→φI2πrdisplaystyle vec H(r,varphi ,z)=vec e_varphi frac I2pi r

umgeben. Die Zirkulation dieses Vektorfeldes entlang eines Kreises r→(φ)=re→r(φ)displaystyle vec r(varphi )=rvec e_r(varphi ) mit φ∈[0,2π)displaystyle varphi in [0,2pi ) und beliebigem positiven Radius rdisplaystyle r ist gleich dem Strom Idisplaystyle I:

∮W⁡H→(r→)⋅dr→=∫φ=02πe→φI2πr⋅re→φdφ=I.displaystyle oint _Wvec H(vec r)cdot mathrm d vec r=int _varphi =0^2pi vec e_varphi frac I2pi rcdot rvec e_varphi mathrm d varphi =I.

Dieses Beispiel demonstriert, dass für die Anwendbarkeit des Stokes'schen Integralsatzes das betreffende Vektorfeld auf einer von der geschlossenen Kurve berandeten Fläche differenzierbar sein muss.
Das Vektorfeld H→displaystyle vec H aus diesem Beispiel ist auf der zdisplaystyle z-Achse nicht definiert. Die Zirkulation wird jedoch entlang eines Kreises gebildet, der die zdisplaystyle z-Achse umschließt. Der Stokes'sche Integralsatz ist also in diesem Fall nicht anwendbar. Das bestätigt sich dadurch, dass die Zirkulation von H→displaystyle vec H entlang des Kreises den von null verschiedenen Wert Idisplaystyle I hat, obwohl das Vektorfeld H→displaystyle vec H auf seinem gesamten Definitionsgebiet rotationsfrei ist (rotH→(r,φ,z)=0→displaystyle operatorname rot ;vec H(r,varphi ,z)=vec 0 für r>0displaystyle r>0).

Komplexe Zirkulation längs eines Kreises in einem Strudel |

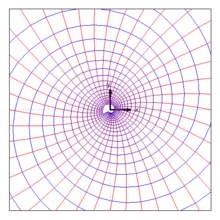
Stromlinien (blau) eines Strudels

Sei

w(z)=Q−iΓ2πzdisplaystyle w(z)=frac Q-mathrm i ,Gamma 2pi z

das komplexe Geschwindigkeitsfeld eines Strudels mit Zentrum bei z=0displaystyle z=0, siehe das Bild und Potentialströmung. Die komplexe Zirkulation der Geschwindigkeit w(z)displaystyle w(z) längs eines Kreises mit Radius Rdisplaystyle R um den Ursprung verschwindet nicht, weil die Geschwindigkeit bei z=0displaystyle z=0 nicht komplex differenzierbar ist und der Kreis diesen Punkt umschließt. Die komplexe Zirkulation der Geschwindigkeit längs des Weges

W:φ∈[0,2π)↦z(φ)=Reiφdisplaystyle Wcolon varphi in [0,2pi )mapsto z(varphi )=Re^mathrm i ,varphi

berechnet sich mit dem Differential dz=iReiφdφdisplaystyle mathrm d z=mathrm i ,Re^mathrm i ,varphi ,mathrm d varphi zu

ΓC=∮W⁡w(z)dz=∮02π⁡Q−iΓ2πReiφiReiφdφ=iQ−iΓ2π∮02πdφ=Γ+iQ.displaystyle Gamma _C=oint _Ww(z),mathrm d z=oint _0^2pi frac Q-mathrm i ,Gamma 2pi Re^mathrm i ,varphi ,mathrm i ,Re^mathrm i ,varphi ,mathrm d varphi =mathrm i ,frac Q-mathrm i ,Gamma 2pi oint _0^2pi ,mathrm d varphi =Gamma +mathrm i ,Q,.mathrmi,R e^mathrmi,varphi,mathrmdvarphi
= "mathrmi,fracQ-mathrmi,Gamma2pi oint_0^2pi,mathrmdvarphi"
="Gamma+mathrmi,Q,."
"/>

Längs des Kreises hat die Geschwindigkeit also unabhängig vom gewählten Radius Rdisplaystyle R immer die Zirkulation Γdisplaystyle Gamma und die Quellstärke Qdisplaystyle Q, die angibt wie groß der über den Kreis tretende Volumenstrom ist. Die komplexe Zirkulation der Geschwindigkeit längs der Kreise ist für alle Kreise gleich, weil die Geschwindigkeit im Kreisring zwischen zwei beliebigen Kreisen immer komplex differenzierbar ist.

Auch hier ist das Geschwindigkeitsfeld außerhalb des Ursprungs rotationsfrei, weil der Strudel eine Potentialströmung ist.

Literatur |

• Königsberger: Analysis 2. Springer-Verlag Berlin, 1993. ISBN 3-540-54723-1.


• Theodore Frankel: The Geometry of Physics (An Introduction). Cambridge University Press, 1997. ISBN 0-521-38753-1.


• Michael Bestehorn: Hydrodynamik und Strukturbildung. Springer, Berlin u. a. 2006, ISBN 3-540-33796-2.